Para Eudoxus de Cnido (c. 400-350 aC), a honra de ser o primeiro a mostrar que a área de um círculo é proporcional ao quadrado do seu raio. Na notação algébrica de hoje, essa proporcionalidade é expressa pela fórmula familiar A = πr 2. No entanto, a constante de proporcionalidade, π, apesar de sua familiaridade, é altamente misteriosa, e a busca para entendê-la e descobrir seu valor exato ocupa matemáticos há milhares de anos. Um século após Eudoxus, Arquimedes encontrado o primeiro boa aproximação de π: 3 10 / 71 <π <3 1 / 7. Ele conseguiu isso aproximando um círculo com um polígono de 96 lados (ver animação). Aproximações ainda melhores foram encontradas usando polígonos com mais lados, mas estes apenas serviram para aprofundar o mistério, porque nenhum valor exato poderia ser alcançado e nenhum padrão pôde ser observado na sequência de aproximações.
Uma solução impressionante do mistério foi descoberto por matemáticos indianos cerca de 1500 ce: π pode ser representado pela infinita, mas surpreendentemente simples, série π / 4 = 1 - 1 / 3 + 1 / 5 - 1 / 7 + ⋯.que descoberto isto como um caso especial da série para a função tangente inversa: tan -1 (x) = x - x 3 / 3 + x 5 / 5 - x 7 / 7 + ⋯.
Os descobridores individuais desses resultados não são conhecidos com certeza; alguns estudiosos os creditam a Nilakantha Somayaji, outros a Madhava. As provas indianas são estruturalmente semelhantes às mais tarde descobertas na Europa por James Gregory, Gottfried Wilhelm Leibniz e Jakob Bernoulli. A principal diferença é que, onde os europeus tinham a vantagem do teorema fundamental do cálculo, os índios tinham que encontrar limites de somas da forma
Antes da redescoberta por Gregory da série de tangentes inversas por volta de 1670, outras fórmulas para π foram descobertas na Europa. Em 1655 John Wallis descoberto o produto infinito π / 4 = 2 / 3 ∙ 4 / 3 ∙ 4 / 5 ∙ 6 / 5 ∙ 6 / 7 ⋯, e o seu colega William Brouncker transformado esta na fracção contínua infinita
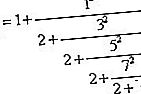
Finalmente, na introdução de Euler para Análise da Infinito (1748), a série π / 4 = 1 - 1 / 3 + 1 / 5 - 1 / 7 + ⋯ é transformado em fracção contínua de Brouncker, que mostra que todos os três fórmulas estão em alguns sentem o mesmo.
A fração infinita e contínua de Brouncker é particularmente significativa porque sugere que π não é uma fração comum - em outras palavras, que π é irracional. Precisamente, essa idéia foi usada na primeira prova de que π é irracional, dada por Johann Lambert em 1767.