Análise tensorial, ramo da matemática relacionado a relações ou leis que permanecem válidas, independentemente do sistema de coordenadas usado para especificar as quantidades. Tais relações são chamadas covariantes. Os tensores foram inventados como uma extensão de vetores para formalizar a manipulação de entidades geométricas surgidas no estudo de variedades matemáticas.
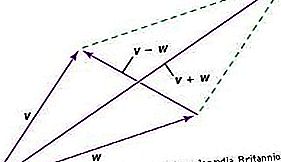
Um vetor é uma entidade que possui magnitude e direção; é representável pelo desenho de uma flecha e combina com entidades semelhantes de acordo com a lei do paralelogramo. Por causa dessa lei, um vetor tem componentes - um conjunto diferente para cada sistema de coordenadas. Quando o sistema de coordenadas é alterado, os componentes do vetor mudam de acordo com uma lei matemática de transformação dedutível da lei do paralelogramo. Essa lei de transformação dos componentes tem duas propriedades importantes. Primeiro, após uma sequência de alterações que acabam no sistema de coordenadas original, os componentes do vetor serão os mesmos que no início. Segundo, as relações entre vetores - por exemplo, três vetores U, V, W, de modo que 2U + 5V = 4W - estarão presentes nos componentes, independentemente do sistema de coordenadas.
Portanto, um vetor pode ser considerado uma entidade que, no espaço n-dimensional, possui n componentes que se transformam de acordo com uma lei específica de transformação com as propriedades acima. O próprio vetor é uma entidade objetiva, independente das coordenadas, mas é tratado em termos de componentes com todos os sistemas de coordenadas em pé de igualdade.
Sem insistir em uma imagem pictórica, um tensor é definido como uma entidade objetiva que possui componentes que mudam de acordo com uma lei de transformação que é uma generalização da lei de transformação vetorial, mas que mantém as duas propriedades principais dessa lei. Por conveniência, as coordenadas são geralmente numeradas de 1 a n, e cada componente de um tensor é indicado por uma letra com sobrescritos e subscritos, cada um dos quais assume independentemente os valores de 1 a n. Assim, um tensor representado pelos componentes T ab c teria n 3 componentes, pois os valores de a, bec dependem de 1 a n. Escalares e vetores constituem casos especiais de tensores, o primeiro possuindo apenas um componente por sistema de coordenadas e o segundo possuindo n. Qualquer relação linear entre os componentes de tensores, tais as7R um BCD + 2s um BCD - 3T um BCD = 0, se válida em um sistema de coordenadas, é válido em todo e, assim, representa uma relação que é objectivo e independente de sistemas de coordenadas, apesar da falta de uma representação pictórica.
Dois tensores, chamados tensor métrico e tensor de curvatura, são de particular interesse. O tensor métrico é usado, por exemplo, na conversão de componentes vetoriais em magnitudes de vetores. Para simplificar, considere o caso bidimensional com coordenadas perpendiculares simples. Deixe o vetor V ter os componentes V 1, V 2. Então, pelo teorema de Pitágoras aplicado ao triângulo retângulo OAP, o quadrado da magnitude de V é dado por OP 2 = (V 1) 2 + (V 2) 2.

Escondido nesta equação está o tensor métrico. Está oculto porque aqui consiste de 0 e 1 que não estão escritos. Se a equação for reescrita na forma PO 2 = 1 (V 1) 2 + 0V 1 V 2 + 0V 2 V 1 + 1 (V 2) 2, o conjunto completo de componentes (1, 0, 0, 1) do tensor métrico é aparente. Se forem usadas coordenadas oblíquas, a fórmula para OP 2 assume a forma mais geralOP 2 = g 11 (V 1) 2 + g 12 V 1 V 2 + g 21 V 2 V 1 + g 22 (V 2) 2, as quantidades g 11, g 12, g 21, g 22 sendo os novos componentes do tensor métrico.
A partir do tensor métrico, é possível construir um tensor complicado, chamado tensor de curvatura, que representa os vários aspectos da curvatura intrínseca do espaço n-dimensional ao qual ele pertence.
Os tensores têm muitas aplicações em geometria e física. Ao criar sua teoria geral da relatividade, Albert Einstein argumentou que as leis da física devem ser as mesmas, independentemente do sistema de coordenadas usado. Isso o levou a expressar essas leis em termos de equações de tensores. Já se sabia de sua teoria especial da relatividade que o tempo e o espaço estão tão intimamente inter-relacionados que constituem um espaço-tempo quadridimensional indivisível. Einstein postulou que a gravitação deveria ser representada apenas em termos do tensor métrico do espaço-tempo quadridimensional. Para expressar a lei relativística da gravitação, ele tinha como blocos de construção o tensor métrico e o tensor de curvatura formado a partir dele. Uma vez que ele decidiu se limitar a esses blocos de construção, a própria escassez o levou a uma equação tensorial essencialmente única para a lei da gravitação, na qual a gravitação emergiu não como uma força, mas como uma manifestação da curvatura do espaço-tempo.
Embora os tensores tenham sido estudados anteriormente, foi o sucesso da teoria geral da relatividade de Einstein que deu origem ao atual interesse generalizado de matemáticos e físicos em tensores e suas aplicações.













